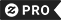Tap / click on image to see more RealViewsTM
$62.10
per tie
Penrose Tiling (Five-Fold Symmetry) Tie
Qty:
About Ties
Sold by
About This Design
Penrose Tiling (Five-Fold Symmetry) Tie
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles. Penrose tilings are named after mathematician and physicist Roger Penrose who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original. Showcase your Penrose tiling sense of style with this necktie featuring reflection symmetry and fivefold rotational symmetry. Perfect tie for any mathematician or physicist with an aperiodic sense of style!
Customer Reviews
4.5 out of 5 stars rating2.4K Total Reviews
2,439 Reviews
Reviews for similar products
5 out of 5 stars rating
By Amy C.17 May 2022 • Verified Purchase
Tie
Zazzle Reviewer Program
It's absolutely perfect!! Turned out much better then I expected ❤️
It is a little expensive but very worth it. Printing is perfect can read it very well
4 out of 5 stars rating
By Anonymous14 September 2025 • Verified Purchase
Tie
I originally ordered 1 tie to test and ensure I liked it with the suits we had ordered! The tie came and it was perfect! We loved it! The colours were bright and the tie was beautifully made. I then ordered the 6 additional ties and the colours are slightly different. The 6 ties were a little less vibrant and the white background was slightly different!
.
5 out of 5 stars rating
By Anonymous6 April 2025 • Verified Purchase
Tie
Lovely. My English class was impressed!
Tags
Other Info
Product ID: 151023638635442023
Added on 1/5/12, 6:12 am
Rating: G
Recently Viewed Items